Uniform Spanning Trees¶
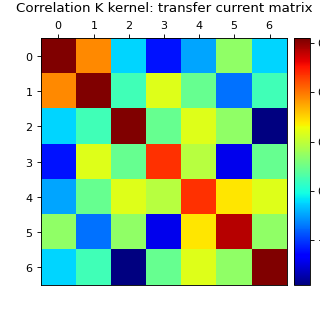
The Uniform measure on Spanning Trees (UST) of a directed connected graph corresponds to a projection DPP with kernel the transfer current matrix of the graph. The later is actually the orthogonal projection matrix onto the row span of the vertex-edge incidence matrix. In fact, one can discard any row of the vertex-edge incidence matrix - note \(A\) the resulting matrix - to compute \(\mathbf{K}=A^{\top}[AA^{\top}]^{-1}A\).
Important
DPPy uses the networkx library to handle DPPs related to trees and graphs, but networkx is not installed by default when installing DPPy. Please refer to the installation instructions on GitHub for more details on how to install the necessary dependencies.
from networkx import Graph
from dppy.exotic_dpps import UST
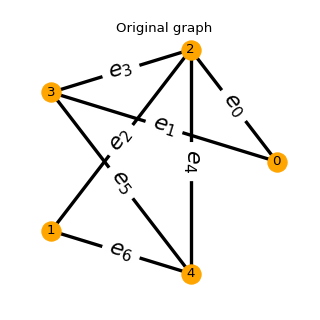
# Build graph
g = Graph()
edges = [(0, 2), (0, 3), (1, 2), (1, 4), (2, 3), (2, 4), (3, 4)]
g.add_edges_from(edges)
# Initialize UST object
ust = UST(g)
# Display underlying kernel i.e. transfer current matrix
ust.plot_graph()
(Source code, png, hires.png, pdf)
# Display underlying kernel i.e. transfer current matrix
ust.plot_kernel()
(Source code, png, hires.png, pdf)
# Display some samples
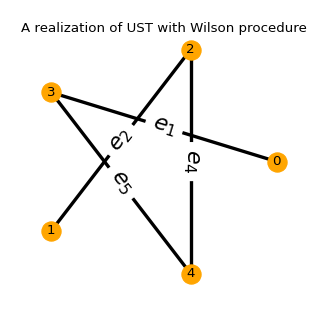
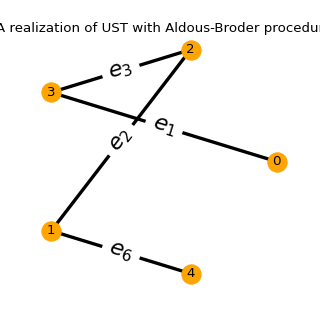
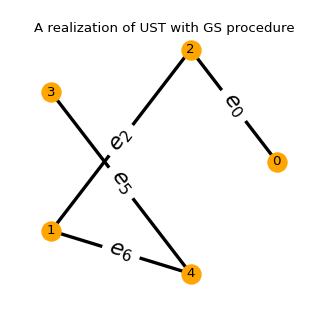
for md in ('Wilson', 'Aldous-Broder', 'GS'):
ust.sample(md)
ust.plot()