Poissonized Plancherel measure¶
The poissonized Plancherel measure is a measure on partitions \(\lambda=(\lambda_1 \geq \lambda_2 \geq \cdots \geq 0)\in \mathbb{N}^{\mathbb{N}^*}\). Samples from this measure can be obtained in the following way
Sample \(N \sim \mathcal{P}(\theta)\)
Sample a uniform permutation \(\sigma\in \mathfrak{S}_N\)
Compute the sorting tableau \(P\) associated to the RSK (Robinson-Schensted-Knuth correspondence) applied to \(\sigma\)
Consider only the shape \(\lambda\) of \(P\).
Finally, the point process formed by \(\{\lambda_i - i + \frac12\}_{i\geq 1}\) is a DPP on \(\mathbb{Z}+\frac12\).
from dppy.exotic_dpps import PoissonizedPlancherel
theta = 500 # Poisson parameter
pp = PoissonizedPlancherel(theta=theta)
pp.sample()
pp.plot_diagram(normalization=True)
(Source code, png, hires.png, pdf)
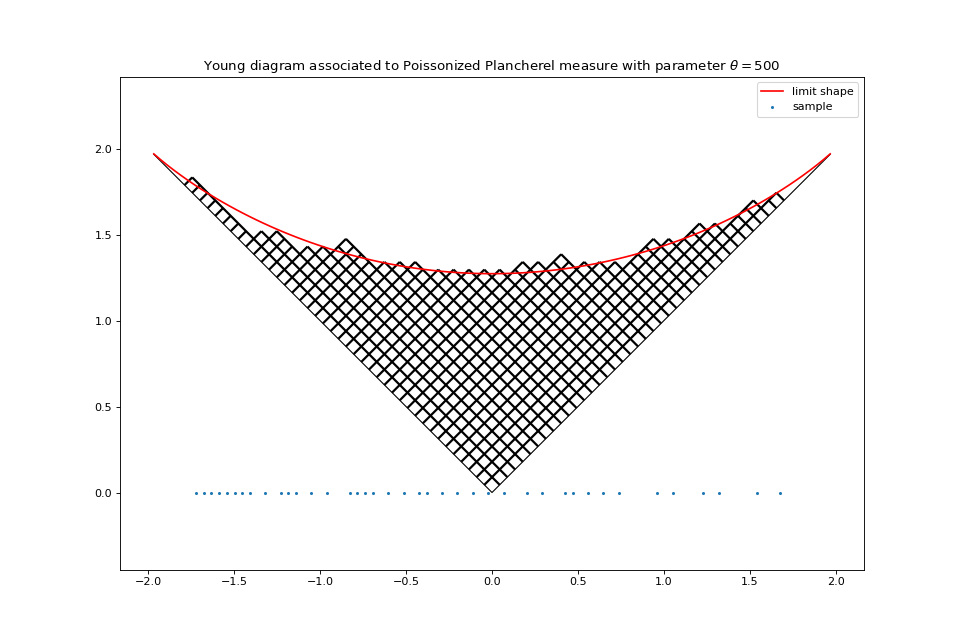
Fig. 54 Poissonized Plancherel measure¶
See also
[Bor09] Section 6