Full matrix models

For specific reference measures the \(\beta = 1, 2, 4\) cases are very singular in the sense that the corresponding ensembles coincide with the eigenvalues of random matrices.

This is a highway for sampling exactly such ensembles in \(\mathcal{O}(N^3)\)!

Hermite Ensemble

Take for reference measure \(\mu=\mathcal{N}(0, 2)\), the pdf of the corresponding \(\beta\)-Ensemble reads

\[ \begin{align}\begin{aligned}(x_1,\dots,x_N) \sim \left|\Delta(x_1,\dots,x_N)\right|^{\beta} \prod_{i= 1}^N e^{- \frac{1}{2}\frac{x_i^2}{2}} % \indic_{\bbR}(x_i) \ d x_i,\\where from the definition in :eq:`eq:abs_vandermonde_det` we have :math:`\left|\Delta(x_1,\dots,x_N)\right| = \prod_{i<j} |x_i - x_j|`.\end{aligned}\end{align} \]

Hint

The Hermite ensemble (whose name comes from the fact that Hermite polynomials are orthogonal w.r.t the Gaussian distribution) refers to the eigenvalue distribution of random matrices formed by i.i.d. Gaussian vectors.

  • \(\beta=1\)

\[X \sim \mathcal{N}_{N, N}(0,1) \qquad A = \frac{X+X^{\top}}{\sqrt{2}}.\]

  • \(\beta=2\)

\[X \sim \mathcal{N}_{N, N}(0,1) + i~ \mathcal{N}_{N, N}(0,1) \qquad A = \frac{X+X^{\dagger}}{\sqrt{2}}.\]

  • \(\beta=4\)

\[\begin{split} \begin{cases} X \sim \mathcal{N}_{N, M}(0,1) + i~ \mathcal{N}_{N, M}(0,1)\\ Y \sim \mathcal{N}_{N, M}(0,1) + i~ \mathcal{N}_{N, M}(0,1) \end{cases} \qquad A = \begin{bmatrix} X & Y \\ -Y^* & X^* \end{bmatrix} \quad A = \frac{X+X^{\dagger}}{\sqrt{2}}.\end{split}\]

Normalization \(\sqrt{\beta N}\) to concentrate as the semi-circle law.

\[\frac{\sqrt{4-x^2}}{2\pi} 1_{[-2,2]} dx.\]
from dppy.beta_ensembles import HermiteEnsemble


hermite = HermiteEnsemble(beta=4)  # beta in {0,1,2,4}, default beta=2
hermite.sample_full_model(size_N=500)
# hermite.plot(normalization=True)
hermite.hist(normalization=True)

# To compare with the sampling speed of the tridiagonal model simply use
# hermite.sample_banded_model(size_N=500)

(Source code, png, hires.png, pdf)

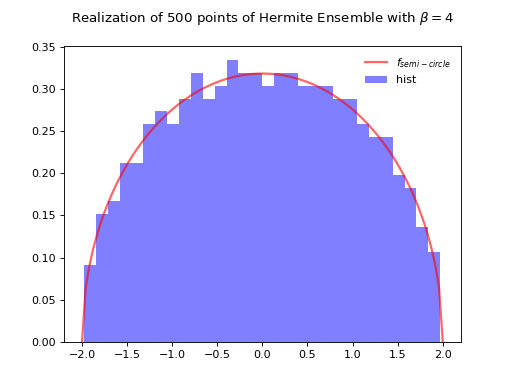
../_images/ex_plot_hermite_full_matrix_model.png

Fig. 8 Full matrix model for the Hermite ensemble

See also

Laguerre Ensemble

Take for reference measure \(\mu=\Gamma\left(\frac{\beta}{2}(M-N+1), 2\right)=\chi_{\beta(M-N+1)}^2\), the pdf of the corresponding \(\beta\)-Ensemble reads

\[ \begin{align}\begin{aligned}(x_1,\dots,x_N) \sim \left|\Delta(x_1,\dots,x_N)\right|^{\beta} % \prod_{i= 1}^N x_i^{\frac{\beta}{2}(M-N+1)-1} e^{- \frac12 x_i} % \indic_{\bbR}(x_i) \ d x_i,\\where from the definition in :eq:`eq:abs_vandermonde_det` we have :math:`\left|\Delta(x_1,\dots,x_N)\right| = \prod_{i<j} |x_i - x_j|`.\end{aligned}\end{align} \]

Hint

The Laguerre ensemble (whose name comes from the fact that Laguerre polynomials are orthogonal w.r.t the Gamma distribution) refers to the eigenvalue distribution of empirical covariance matrices of i.i.d. Gaussian vectors.

  • \(\beta=1\)

\[X \sim \mathcal{N}_{N, M}(0,1) \qquad A = XX^{\top}.\]

  • \(\beta=2\)

\[X \sim \mathcal{N}_{N, M}(0,1) + i~ \mathcal{N}_{N, M}(0,1) \qquad A = XX^{\dagger}.\]

  • \(\beta=4\)

\[\begin{split} \begin{cases} X \sim \mathcal{N}_{N, M}(0,1) + i~ \mathcal{N}_{N, M}(0,1)\\ Y \sim \mathcal{N}_{N, M}(0,1) + i~ \mathcal{N}_{N, M}(0,1) \end{cases} \qquad A = \begin{bmatrix} X & Y \\ -Y^* & X^* \end{bmatrix} \quad A = A A^{\dagger}.\end{split}\]

Normalization \(\beta M\) to concentrate as Marcenko-Pastur law.

\[\frac{1}{2\pi} \frac{\sqrt{(\lambda_+-x)(x-\lambda_-)}}{cx} 1_{[\lambda_-,\lambda_+]} dx,\]

where

\[c = \frac{M}{N} \quad \text{and} \quad \lambda_\pm = (1\pm\sqrt{c})^2.\]
from dppy.beta_ensembles import LaguerreEnsemble


laguerre = LaguerreEnsemble(beta=1)  # beta in {0,1,2,4}, default beta=2
laguerre.sample_full_model(size_N=500, size_M=800)  # M >= N
# laguerre.plot(normalization=True)
laguerre.hist(normalization=True)

# To compare with the sampling speed of the tridiagonal model simply use
# laguerre.sample_banded_model(size_N=500, size_M=800)

(Source code, png, hires.png, pdf)

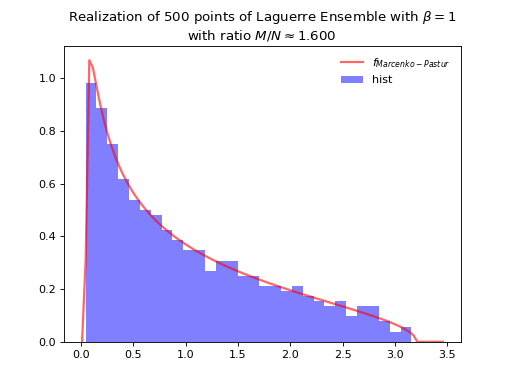
../_images/ex_plot_laguerre_full_matrix_model.png

Fig. 10 Full matrix model for the Laguerre ensemble

See also

Jacobi Ensemble

Take for reference measure \(\mu=\operatorname{Beta}\left(\frac{\beta}{2}(M_1-N+1), \frac{\beta}{2}(M_2-N+1)\right)\), the pdf of the corresponding \(\beta\)-Ensemble reads

\[ \begin{align}\begin{aligned}(x_1,\dots,x_N) \sim \left|\Delta(x_1,\dots,x_N)\right|^{\beta} % \prod_{i= 1}^N x_i^{\frac{\beta}{2}(M_1-N+1)-1} (1-x_i)^{\frac{\beta}{2}(M_2-N+1)-1} % \indic_{\bbR}(x_i) \ d x_i,\\where from the definition in :eq:`eq:abs_vandermonde_det` we have :math:`\left|\Delta(x_1,\dots,x_N)\right| = \prod_{i<j} |x_i - x_j|`.\end{aligned}\end{align} \]

Hint

The Jacobi ensemble (whose name comes from the fact that Jacobi polynomials are orthogonal w.r.t the Beta distribution) is associated with the multivariate analysis of variance (MANOVA) model.

  • \(\beta=1\)

\[\begin{split}\begin{cases} X \sim \mathcal{N}_{N, M_1}(0,1)\\ Y \sim \mathcal{N}_{N, M_2}(0,1)\\ \end{cases} \qquad A = XX^{\top}\left(XX^{\top} + YY^{\top}\right)^{-1}.\end{split}\]

  • \(\beta=2\)

\[\begin{split}\begin{cases} X \sim \mathcal{N}_{N, M_1}(0,1) + i~ \mathcal{N}_{N, M_1}(0,1)\\ Y \sim \mathcal{N}_{N, M_2}(0,1) + i~ \mathcal{N}_{N, M_2}(0,1)\\ \end{cases} \qquad A = XX^{\dagger}\left(XX^{\dagger} + YY^{\dagger}\right)^{-1}.\end{split}\]

  • \(\beta=4\)

\[\begin{split} \begin{cases} X_1 \sim \mathcal{N}_{N, M_1}(0,1) + i~ \mathcal{N}_{N, M_1}(0,1)\\ X_2 \sim \mathcal{N}_{N, M_1}(0,1) + i~ \mathcal{N}_{N, M_1}(0,1)\\ Y_1 \sim \mathcal{N}_{N, M_2}(0,1) + i~ \mathcal{N}_{N, M_2}(0,1)\\ Y_2 \sim \mathcal{N}_{N, M_2}(0,1) + i~ \mathcal{N}_{N, M_2}(0,1) \end{cases} \qquad \begin{cases} X = \begin{bmatrix} X_1 & X_2 \\ -X_2^* & X_1^* \end{bmatrix}\\ Y = \begin{bmatrix} Y_1 & Y_2 \\ -Y_2^* & Y_1^* \end{bmatrix} \end{cases} \qquad A = XX^{\dagger}\left(XX^{\dagger} + YY^{\dagger}\right)^{-1}.\end{split}\]

Concentrates as Wachter law

\[\frac{(a+b)\sqrt{(\sigma_+-x)(x-\sigma_-)}}{2\pi x(1-x)}dx,\]

where

\[a = \frac{M_1}{N}, b = \frac{M_2}{N} \quad\text{and}\quad \sigma_{\pm} = \left(\frac{\sqrt{a(a+b-1)} \pm \sqrt{b}}{a+b}\right)^2,\]

itself tending to the arcsine law in the limit.

from dppy.beta_ensembles import JacobiEnsemble


jacobi = JacobiEnsemble(beta=2)  # beta must be in {0,1,2,4}, default beta=2
jacobi.sample_full_model(size_N=400, size_M1=500, size_M2=600)  # M_1, M_2 >= N
# jacobi.plot(normalization=True)
jacobi.hist(normalization=True)

# To compare with the sampling speed of the triadiagonal model simply use
# jacobi.sample_banded_model(size_N=400, size_M1=500, size_M2=600)

(Source code, png, hires.png, pdf)

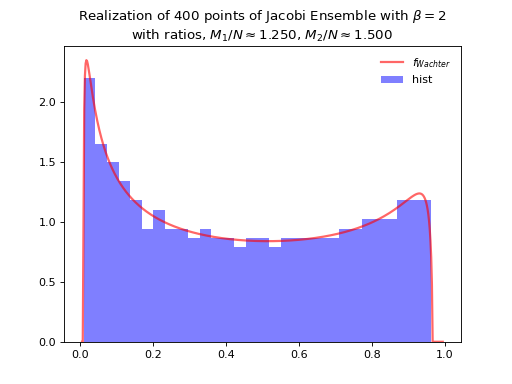
../_images/ex_plot_jacobi_full_matrix_model.png

Fig. 12 Full matrix model for the Jacobi ensemble

See also

Circular Ensemble

\[ \begin{align}\begin{aligned} \left|\Delta(e^{i \theta_1 },\dots, e^{i \theta_N})\right|^{\beta} \prod_{j = 1}^N \frac{1}{2\pi} \mathbf{1}_{[0,2\pi]} (\theta_j) d\theta_j,\\where from the definition in :eq:`eq:abs_vandermonde_det` we have :math:`\left|\Delta(x_1,\dots,x_N)\right| = \prod_{i<j} |x_i - x_j|`.\end{aligned}\end{align} \]

Hint

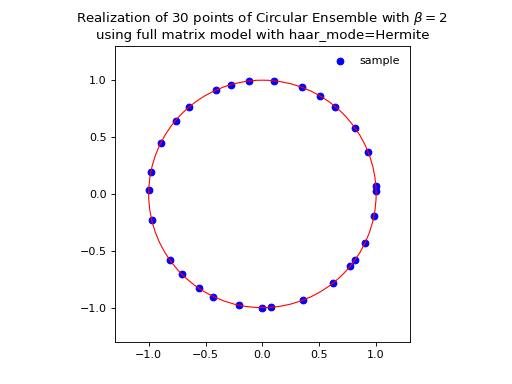
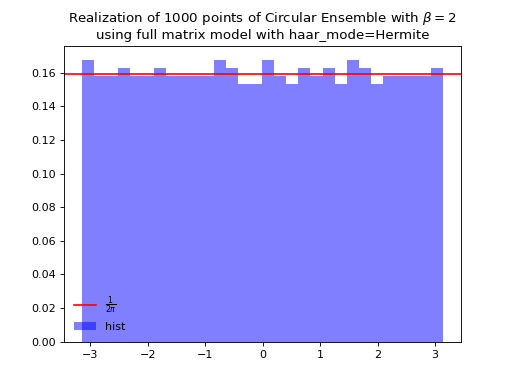
Eigenvalues of orthogonal (resp. unitary and self-dual unitary) matrices drawn uniformly i.e. Haar measure on the respective groups. The eigenvalues lie on the unit circle i.e. \(\lambda_n = e^{i \theta_n}\). The distribution of the angles \(\theta_n\) converges to the uniform measure on \([0, 2\pi[\) as \(N\) grows.

  • \(\beta=1\)

    Uniform measure i.e. Haar measure on orthogonal matrices \(\mathbb{O}_N\): \(U^{\top}U = I_N\)

    1. Via QR algorithm, see [Mez06] Section 5

    import numpy as np
from numpy.random import randn
import scipy.linalg as la

A = randn(N, N)
Q, R = la.qr(A)
d = np.diagonal(R)
U = np.multiply(Q, d/np.abs(d), Q)
la.eigvals(U)

    1. The Hermite way

    \[\begin{split} X \sim \mathcal{N}_{N, N}(0,1)\\ A = X+X^{\top} = U^{\top}\Lambda U\\ eigvals(U).\end{split}\]

  • \(\beta=2\)

    Uniform measure i.e. Haar measure on unitary matrices \(\mathbb{U}_N\): \(U^{\dagger}U = I_N\)

    1. Via QR algorithm, see [Mez06] Section 5

    import numpy as np
from numpy.random import randn
import scipy.linalg as la

A = randn(N, N) + 1j*randn(N, N)
Q, R = la.qr(A)
d = np.diagonal(R)
U = np.multiply(Q, d / np.abs(d), Q)
la.eigvals(U)

    from dppy.beta_ensembles import CircularEnsemble

circular = CircularEnsemble(beta=2)  # beta in {0,1,2,4}, default beta=2

# 1. Plot the eigenvalues, they lie on the unit circle
circular.sample_full_model(size_N=30, haar_mode='QR')
circular.plot()

# 2. Histogram of the angle of more points, should look uniform on [0,2pi]
circular.flush_samples()  # Flush previous sample

circular.sample_full_model(size_N=1000, haar_mode='QR')
circular.hist()

    (Source code)

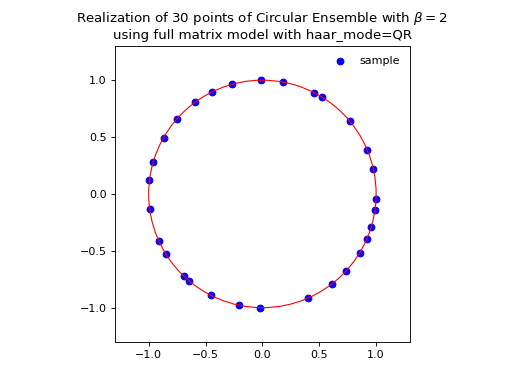
    ../_images/ex_plot_circular_full_matrix_model_qr_00.png

    Fig. 14 (png, hires.png, pdf) Full matrix model for the Circular ensemble from QR on random Gaussian matrix

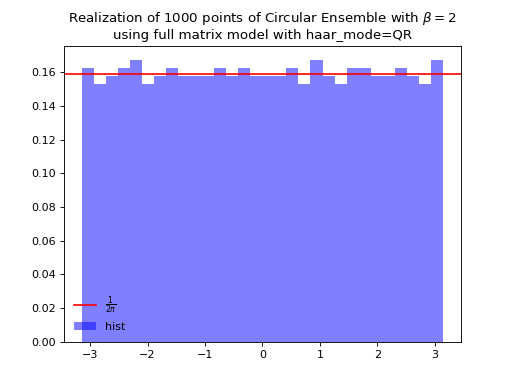
    ../_images/ex_plot_circular_full_matrix_model_qr_01.png

    Fig. 15 (png, hires.png, pdf) Full matrix model for the Circular ensemble from QR on random Gaussian matrix

    1. The Hermite way

    \[\begin{split} X \sim \mathcal{N}_{N, N}(0,1) + i~ \mathcal{N}_{N, N}(0,1)\\ A = X+X^{\dagger} = U^{\dagger}\Lambda U\\ eigvals(U).\end{split}\]
    from dppy.beta_ensembles import CircularEnsemble

circular = CircularEnsemble(beta=2)  # beta in {0,1,2,4}, default beta=2

# 1. Plot the eigenvalues, they lie on the unit circle
circular.sample_full_model(size_N=30, haar_mode='Hermite')
circular.plot()

# 2. Histogram of the angle of more points, should look uniform on [0,2pi]
circular.flush_samples()  # Flush previous sample

circular.sample_full_model(size_N=1000, haar_mode='Hermite')
circular.hist()

    (Source code)

    ../_images/ex_plot_circular_full_matrix_model_hermite_00.png

    Fig. 18 (png, hires.png, pdf) Full matrix model for the Circular ensemble from Hermite matrix

    ../_images/ex_plot_circular_full_matrix_model_hermite_01.png

    Fig. 19 (png, hires.png, pdf) Full matrix model for the Circular ensemble from Hermite matrix

  • \(\beta=4\)

    Uniform measure i.e. Haar measure on self-dual unitary matrices \(\mathbb{U}\operatorname{Sp}_{2N}\): \(U^{\dagger}U = I_{2N}\)

    \[\begin{split} \begin{cases} X \sim \mathcal{N}_{N, M}(0,1) + i~ \mathcal{N}_{N, M}(0,1)\\ Y \sim \mathcal{N}_{N, M}(0,1) + i~ \mathcal{N}_{N, M}(0,1) \end{cases}\\ A = \begin{bmatrix} X & Y \\ -Y^* & X^* \end{bmatrix} \quad A = X+X^{\dagger} = U^{\dagger} \Lambda U\\ eigvals(U).\end{split}\]

See also

Ginibre Ensemble

\[\left|\Delta(z_1,\dots,z_N)\right|^{2} \prod_{i = 1}^N e^{ - \frac{1}{2}|z_i|^2 } d z_i,\]

where from the definition in (33) we have \(\left|\Delta(x_1,\dots,x_N)\right| = \prod_{i<j} |x_i - x_j|\).

\[A \sim \frac{1}{\sqrt{2}} \left( \mathcal{N}_{N,N}(0,1) + i~ \mathcal{N}_{N, N}(0,1) \right).\]

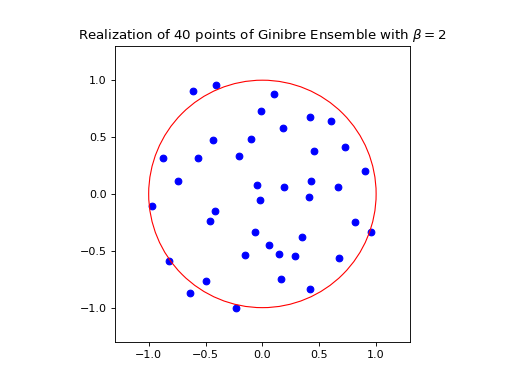
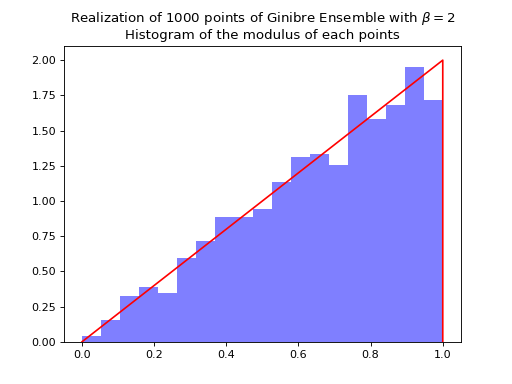
Nomalization \(\sqrt{N}\) to concentrate in the unit circle.

from dppy.beta_ensembles import GinibreEnsemble


ginibre = GinibreEnsemble()  # beta must be 2 (default)

ginibre.sample_full_model(size_N=40)
ginibre.plot(normalization=True)

ginibre.sample_full_model(size_N=1000)
ginibre.hist(normalization=True)

(Source code)

../_images/ex_plot_ginibre_full_matrix_model_00.png

Fig. 22 (png, hires.png, pdf) Full matrix model for the Ginibre ensemble

../_images/ex_plot_ginibre_full_matrix_model_01.png

Fig. 23 (png, hires.png, pdf) Full matrix model for the Ginibre ensemble

See also